Quantum Computer
The Quantum Computer
By Vijay Kumar
"If scientists built a quantum computer, it would be able to perform calculations with such enormous speed that it would make a modern computer look like a broken abacus." - Simone Singh, Author of science non-fiction books like Fermat's Last Theorem, The Code Book.
"Anyone who can contemplate quantum mechanics without getting dizzy hasn't understood it." - Niels Bohr, one of the fathers of quantum mechanics.
The first quote by Simone Singh might have evoked your interest in quantum computer, while the second one by Niels Bohr might have had the reverse effect. Well, this article does not dwell into the dizzy theories of quantum computers in detail, but is a presentation of the bizarre scientific theories about quantum concept that Simone Singh put in a very simple manner in his book - The Code Book, which primarily deals with cryptography.
Superposition and many-world interpretation
In order to explain the principles of quantum computing, it helps to recollect the infamous "Thomas Young Experiment" that we all would have learnt in school. The experiment is very simple. Take a source of light and shine it on a screen with two parallel small slits, allow the light coming out of these slits to illuminate a screen several meters away. You would observe a striped pattern of light on the screen as shown in the diagram 1 (ThomasYoung.gif). Assuming that light consists of countless individual particles, known as photons, which exhibit wave-like properties (combination of particle and wave theory), this phenomenon was explained as follows: "The waves from the two slits interfere with each other and at point of interference of the peak of two waves a bright light is produced, while at the point of interaction of two troughs a dark patch is produced."
|
Thomas Young's Double Slit Experiment
|
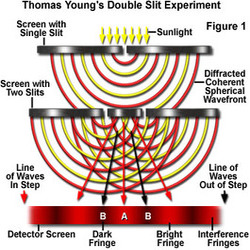 |
So far there is nothing strange about this experiment. However, modern technology allows physicists to repeat Young's experiment using a filament that is so dim that it emits single photons of light. Young's experiment was repeated with a single photon passed through one of the two slits. With this setup we would not expect to see the striped pattern as observed before. However, for some extraordinary reason, even with single photons the result of the screen is still a pattern of light and dark stripes, just as if photons had been interacting!
This result defies common sense. There is no way to explain this phenomenon in terms of classical physics. In order to explain this phenomenon, physicists tried to find answers in quantum physics. However even quantum theorists also could not agree on the interpretation of this experiment. There were two different groups, each with their own interpretations.
One interpretation is known as superposition. The superpositionists state that if we do not know what a particle is doing, then it is allowed to do everything possible simultaneously. In case of the photon, we don't know whether it passed thought he left slit of the right slit, so we assume that it passed through both the slits simultaneously, possibly by splitting up into two "ghost" photons. These interact to produce the stripe pattern. Though it sounds silly, it at least explains the striped pattern.
Erwin Schrödinger, who won the Nobel Prize for Physics in 1933, invented a parable known as Schrödinger's cat, which is often used to explain the concept of superposition. Imagine a living cat in a thick lead box. At this stage, there is no question that the cat is alive. We then throw in a vial of cyanide and seal the box. We do not know if the cat is alive or if it has broken the cyanide capsule and died. Since we do not know, the cat can be both, dead and alive, according to quantum law, the cat is in a superposition of state. It is only when we break open the box and learn the condition of the cat that the superposition is lost, and the cat becomes one or the other - dead or alive.
Another theory is the many-worlds interpretation. According to this theory, upon leaving the filament the photon has two choices; it either enter the left slit or the right slit - at which point the universe divides into two universes. In one universe the photon goes through the left slit, and in the other universe the photon goes through the right slit. These two universes somehow interfere with each other, which accounts for the striped pattern.
Atoms and quantum physics
One classic phenomenon unanswered by classic physics is 'Why don't atoms crash into the nucleus?'
If electrons orbit around the nucleus and Newton's gravity concept is considered, then they should spiral inward and crash into it, in a fraction of a second, destroying the atom. Ernest Rutherford, when he discovered the atomic nucleus in 1911/2, proposed that electrons don't fall into the nucleus for the same reason that planets don't fall into the sun: their velocity is sufficient to exactly balance the attraction exerted, and so they maintain orbits. This proposal was called the solar system model of the atom.
Keeping a planet or an electron in an orbit involves a continuous acceleration: the object's velocity is constantly changed (in direction) in order to maintain the orbital curve.
Unfortunately, Maxwell's Equations say that accelerating an electric charge results in the emission of electromagnetic radiation (light energy). An orbiting electron would radiate its orbital energy away, and fall into the nucleus in something like a picosecond.
Nothing could explain why this doesn't happen, at least until quantum physics came onto the scene 70 years ago. The quantum physics solution proposed by Niels Bohr is fairly simple, the election isn't actually orbiting around the atom, in reality it isn't anywhere at all, there is simply a probability of it being somewhere. The diagram 2 (electron.gif ) shows you the probability of an electron being somewhere around the atom. The black spots show you where it is likely to be while the white bits are where it is very unlikely to be. The electron doesn't orbit around the atom, it simply jumps around the atom randomly, although of course it is more likely to be in certain places than others as shown here.
|
Quantum Electron
|
|
|
Does this mean that classical physics is useless? The answer is that classic physics does have problems, but they only show up when you look at single atoms or other really small things (subatomic level). For big things, classical physics works quite well. And also classical physics is easier to comprehend.
The Quantum Computer
Of all consequences of quantum theory, the most important is potentially the quantum computer. Imagine you have two versions of a question, to answer both questions using an ordinary computer; you would have to input the first version and wait for the answer, then input the second version and wait for the answer. In other words, an ordinary computer can address only one question at a time, and if there are several questions it has to address then, it would have to do it sequentially. However, with a quantum computer, the two questions could be combined as a superposition of two states and inputted simultaneously - the machine itself would then enter a superposition of the two states, one for each question. Or, according to the many-worlds interpretation, the machine would enter two different universes, and answer each version of the question in a different universe. Regardless of the interpretation, the quantum computer can address two questions at the same time by exploiting the laws of quantum physics.
To get an idea of the power of quantum computer, we can compare its performance with that of a traditional computer by seeing what happens when each is used to tackle a particular problem.
The problem - Find a number whose square and cube together use all the digits 0-9 without repetition.
Example: 192 = 391 and 193 = 6859. This does not fit the requirement, since digits 0,2,4,7 are missing and digit 6 is repeated.
Traditional Computer: Check number 1, then number 2, then number 3 ... number 68, then number 69. Get the answer! (692=4761 and 693 = 328509). Assuming each check takes about 1 second, the entire process takes 69 seconds.
Quantum Computer: Check all numbers at once (using superposition or the many-worlds interpretation). Result got in 1 sec!
Extending the same principle to cryptography, quantum computers can break and decipher data encrypted by the strongest algorithms (considered to be unbreakable even if all the atoms in the universe were a computer capable of performing trillion calculations per millisecond) known today, in a matter of seconds!
Conventional scientists dread the theory of quantum physics (on which the discussions of quantum computer is based) since it breaks the fundamental laws of classical physics and provides answers to some unanswered questions.
Practically quantum computers remain in a primitive form and confined to laboratories and are pursued by very few scientific minds that can adapt to bizarre ideas. Convincing the world of quantum concepts has been the greatest challenge to such individuals.
Only time will tell if when the quantum computer can become a reality. At this point in time we can merely speculate as to what impact it can have. Taking the example of cryptography, as information becomes the world's most valuable commodity, the economic, political and military fate of nations will depend on the strength of ciphers (encrypted data). Consequently, the development of a fully operational quantum computer would peril our personal privacy, destroy electronic commerce and demolish national security. In short a quantum computer would jeopardize the stability of the world!
out the author:
Vijay Kumar L K, is a Project Engineer with the Manufacturing domain, currently working on a project on Company Registry Services for Sun Microsystems IS. His interests include teaching, music, cryptography, Quantum theories and anything regarding the movie Matrix. He has also authored an article titled .
